НЕКОТОРЫЕ ОСОБЕННОСТИ РАСПРЕДЕЛЕНИЯ ТОЧЕК
НА ЗЕМНОЙ ПОВЕРХНОСТИ
В.П.Жарков
Москва, 2001 г.
В действительности все выглядит иначе,
чем на самом деле.
(Станислав Ежи Лец)
Часть 1
Введение
Целью данной работы является попытка найти возможные закономерности распределения точек на земной поверхности для выделенных регионов с точки зрения некоторых вероятностных функций.
Первоначальной задачей была простая проверка фактов, изложенных в [3] стр.249 и связанных с расположением большинства европейских столиц. Результат (явившийся несколько неожиданным даже для автора) привел к необходимости некоторого количественного анализа и сравнения нескольких регионов. Автор предлагает считать этот результат фактом, вне зависимости от его трактовки.
Работа предполагает знакомство читателя с теорией вероятности в объеме технического ВУЗа. Используемые формулы и некоторые подробности приведены в Приложении 2.
Постановка задачи, исходные данные
На поверхности шара в некоторых территориально обособленных регионах каким-то образом расположены точки. Для каждой точки региона выдвигается гипотеза о случайном распределении остальных точек по отношению к ней. Оценивается вероятность этой гипотезы. Регионы исследуются последовательно. Результат оценки представляется графически.
Для рассмотрения выбираются следующие регионы и точки:
1. Европа и Ближний Восток. Столицы государств.
2. Европа. Столицы государств.
3. Азия. Столицы государств.
4. Африка. Столицы государств.
5. Северная Америка. Столицы штатов США.
6. Южная Америка. Столицы государств.
Земная поверхность аппроксимируется шаром с радиусом, равным среднему радиусу эллипсоида Красовского ([2] стр.255), что позволяет определять расстояния в выбранных регионах с погрешностью не более 5%.
Координаты точек сняты с [1] с точностью 0.1 градуса.
Все используемые при расчетах формулы приведены в [4],[5],[6] либо легко выводятся с их помощью.
Функции, применяемые в исследовании
Для каждого региона производятся следующие действия:
Первым шагом является построение гистограмм расстояний от каждой точки до всех остальных точек. (Для региона 1 это является повторением работы, приведенной в [3] стр.249 и послужившей толчком к написанию данной статьи. Так как автор проводил все расчеты самостоятельно, это можно считать независимой проверкой). Гистограммы расстояний в данной редакции не приводятся из-за большого объема графики и их вспомогательной роли, вместо них приведены таблицы расстояний см. Приложение 1.
На следующем этапе вводятся дискретные функции T(n,k) и pop(m,n,k), строящиеся следующим образом:
1. Для каждой точки региона сводятся в таблицу расстояния до всех остальных точек. Номер точки обозначается n.
2. Для каждой точки в таблице вычисляется максимальное расстояние Lmax(n).
3. Для каждой точки в таблице вычисляется интервал оценки l = Lmax/k, где k задается как параметр. При проведении расчетов использовались значения k от 2 до 8.
4. Для каждой точки интервал l(n,k) смещается с шагом 50км вдоль Lmax(n) от его начала до конца, номер шага обозначается m. При этом подсчитывается и сводится в таблицу количество точек, попадающих в интервал для каждого шага. Эта таблица и определяет значения функции pop(m,n,k). Аргументом служит номер шага.
5. Для каждой точки по значениям pop(m) определяется максимальное значение popmax=max(pop(m)). \
Далее по ф-ле Бернулли определяется вероятность этого события при гипотезе случайного распределения P (popmax). Вычисляется функция T(n,k)= -ln P (popmax).
Для наглядности эти функции изображаются в виде непрерывных кривых, хотя они, естественно, имеют смысл только в определенных точках.
С помощью функции T(n,k) мы получаем возможность сравнить вероятности реальных распределений точек относительно каждой из них.
При этом следует иметь в виду, что чем меньше значение T(n,k), тем ближе распределение к случайному, чем выше - тем меньше вероятность случайного распределения, то есть правомерно рассмотреть гипотезу о проявлении некоего закона.
Можно предположить, что расположение точек определяется одним или несколькими из 2 объективных факторов и одного субъективного:
- географической конфигурацией региона;
- историей его заселения;
- умыслом строителя.
Например, при заселении региона извне (с моря) следует ожидать наибольшего количества точек на побережье, если в центре региона лежит большая слабо заселенная местность (горы, пустыня), точки будут группироваться вокруг нее и т.д.
Некоторые свойства функций Т(n,k) и pop(m,n,k)
Прежде чем приступить к анализу результатов по реальным распределениям, имеет смысл рассмотреть поведение функции Т(n,k) на нескольких вариантах теоретических моделей.
Вариант 1. Распределение точек, показанное на рис.1 (модель с и модель s).
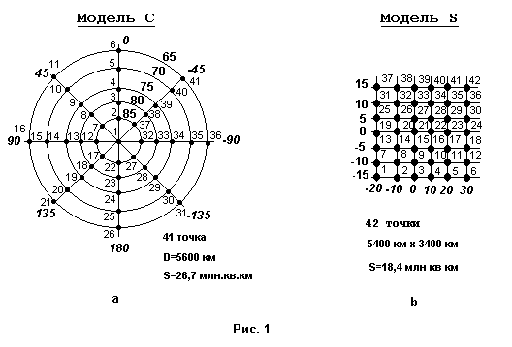
При этом учитывается равенство по порядку количества точек, максимальных расстояний и площади теоретического региона реальным регионам.
Координаты модели смещены на некоторую малую величину, чтобы избежать эффектов, связанных с точными совпадениями.
Поведение Т(n,k) и pop(m,n,k) для модели C и модели S представлено на рис.2 и рис. 3 соответственно. Параметром служит коэффициент деления интервала k=Lmax/l, изменяющийся в интервале 2-8. Для рис. 3 k=4, как дающий наиболее характерный вид.
Дальнейшее увеличение коэффициента ведет к искажениям, связанным с реальной точностью координат и "эффектом невероятного события": теоретическая вероятность попадания в заданную точку при l=0 l/L=0.
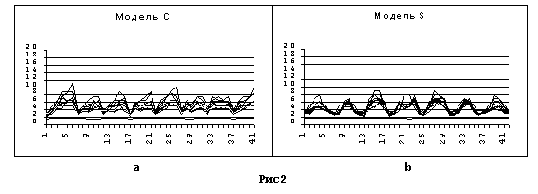
На рис. 2 мы видим, что значения T(n,k) лежат не превышают 12, яркие пики отсутствуют. Рис а показывает, что хотя точки и расположены по окружностям, недостаточное их количество не позволяет выявить их расположение, графики практически похожи. Функция pop(n,k) также имеет "стандартный", ничем не выделяющийся вид : подъем, максимум, спад с несколькими локальными максимумами, как показано на рис. 3.
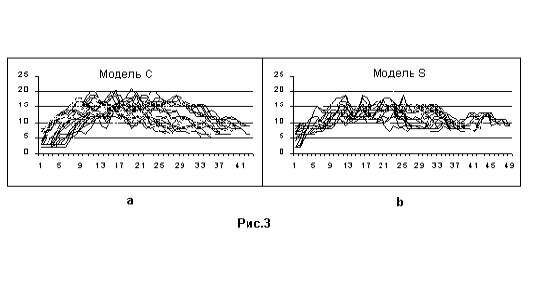
Отметим такое поведение функций как характерное для достаточно равномерного распределения точек.
Вариант 2: Моделирование проводится с выносом одной из точек за пределы региона. Как показывает анализ, результаты для моделей C и S практически одинаковы, поэтому рассмотрим только первую. В данном случае одна из точек (N 6) удаляется примерно на 1/3 диаметра модели. Как видно из Рис. 4 а удаление точки ведет к яркому увеличению пиковых значений T(n,k), причем как для удаленной точки, так и для некоторых точек региона. На графиках pop(m,n,k) на Рис. 4 b, c, d видно появление сильно отличающейся кривой, это как раз кривая для точки 6 (выделена толщиной).
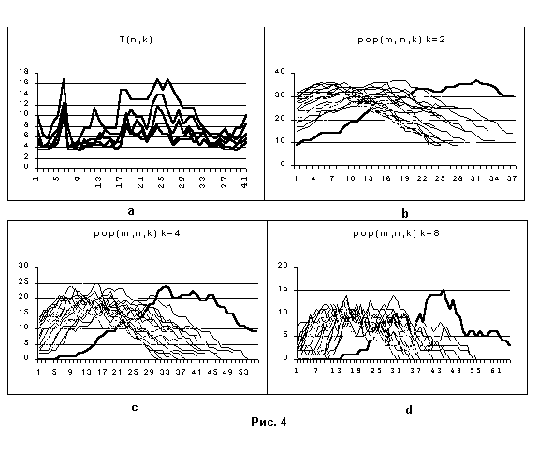
Результат анализа позволяет провести границу между точками региона и точками вне региона (изолированными) по поведению функции pop(m,n,k).
Вариант 4. Рассматривается результат случайного распределения. Выбрана поверхность приблизительно равная поверхности европейско-ближневосточного региона, количество точек 37, координаты выбраны с помощью датчика случайных чисел. Проведено 10 испытаний. Функция T(n,k) для 4 первых для k=2, 4, 6, 8 приведена на Рис. 5, остальные, ввиду их непринципиального отличия, не приводятся.
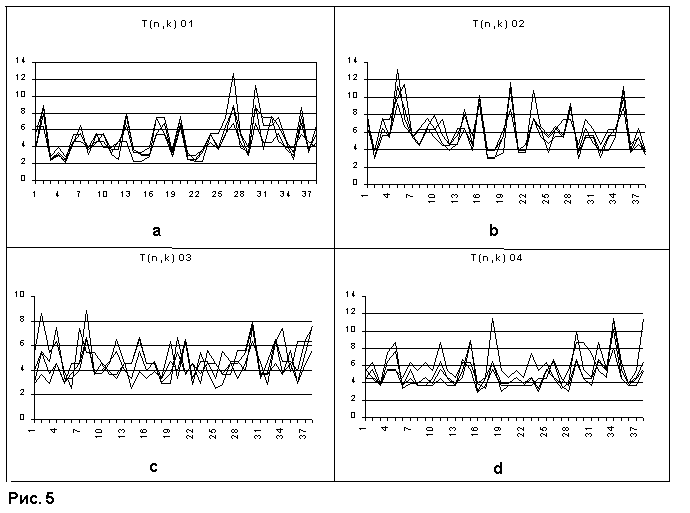
Отметим, что пиковые значения как для равномерных распределений, так и для случайных лежат в диапазоне 8-14, что можно считать для них характерным.
Поведение функции T(n,k) на реальных раcпределениях точек
Рассмотрим выбранные регионы в порядке возрастания интереса. Для каждого из них приводится 2 графика. Первый - значения T(n,k) при k=2,4,6,8 (кривая для k=4 выделена), второй - суммарное значение T(n) при перечисленных k.
Для удобства графики представлены в виде непрерывных кривых. В приложение сведены таблицы расстояний для точек рассматриваемых регионов, к гистограммам которых также может быть полезным обращаться при анализе. Построение их, например, с помощью Excel не представляет никакого труда. Очевидно, максимумам T(n) на гистограммах будут соответствовать участки максимальной длины с наименьшим наклоном.
1. Южная Америка
К сожалению, в Южной Америке на большой территории располагается всего 13 точек, дающих весьма невнятную картину, не позволяющую сделать никаких выводов. Значения T(n,k) ниже значений для случайных распределений.
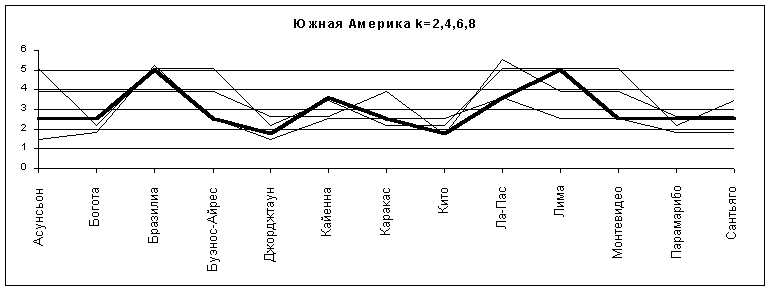
Рис.6
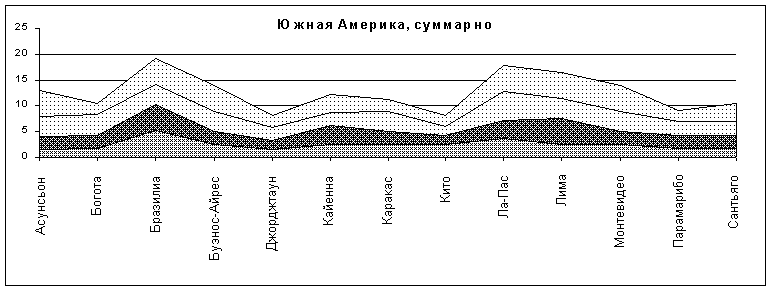
Рис.7
2. Азия
Набор точек здесь достаточно велик однако график близок к графикам случайного распределения. Никаких особенностей не наблюдается.
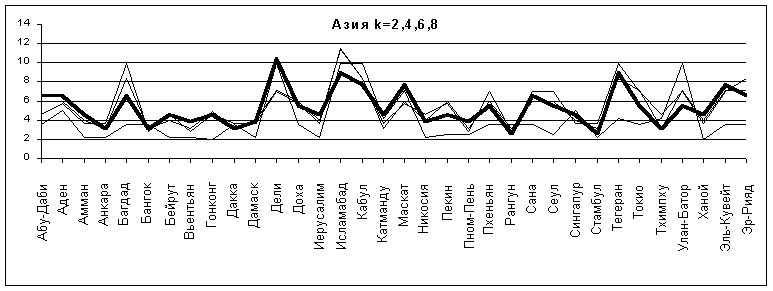
Рис.8
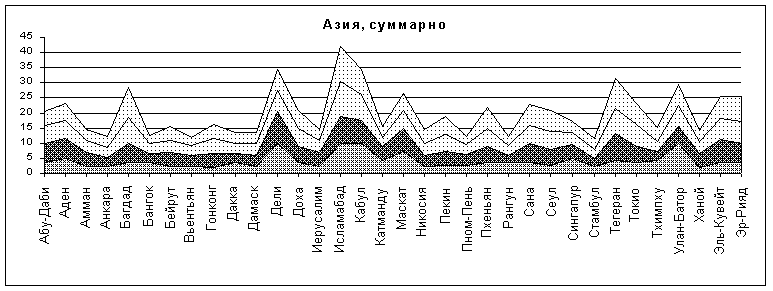
Рис.9
3. Африка
Графики для Африки более выразительны, хотя почти не выходят за пределы случайного распределения. Обратим внимание на максимумы (Триполи, Тунис, Каир). По гистограммам расстояний отмечается, что "слой" точек с максимальной плотностью (приблизительно R=3500 км, толщина около 1500 км) для Каира приходится на северо-западный берег континента, а для Триполи и Туниса на северное побережье Гвинейского залива, это можно увидеть на любой географической карте. Очевидно, что заселение (в смысле строительства населенных пунктов, ставших потом столицами), велось здесь, преимущественно, с моря. Для прочих точек график показывает распределение, близкое к случайному.
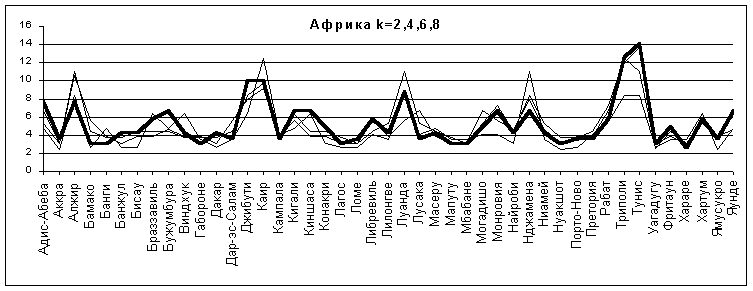
Рис.10
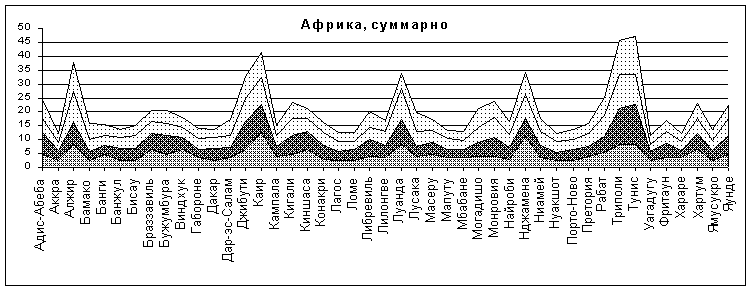
Рис.11
4. США
В распределении для Соединенных Штатов явно выделяется точка Лансинг . По карте можно увидеть, что кольцо со средним радиусом около 1000 км и шириной 700 км охватывает Атлантическое побережье и побережье Мексиканского залива, расположенные в виде грубой полуокружности относительно Лансинга. Этот же факт отражается в менее четких пиках для Нашвилла, Колумбии, Сент-Пола, Чарльстона.
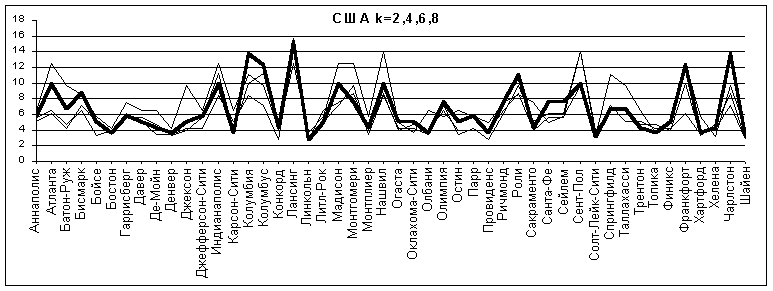
Рис.12
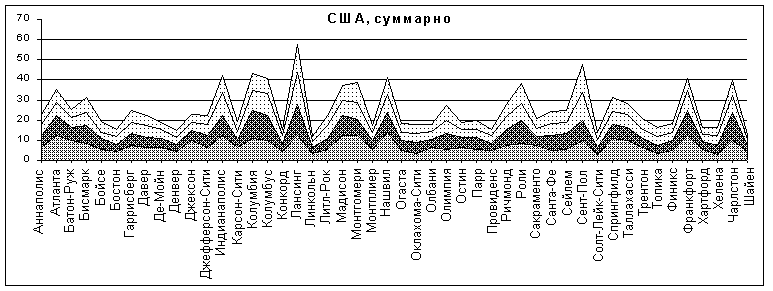
Рис.13
Далее приступим к рассмотрению наиболее интересного региона в 2 вариантах: только европейские столицы и столицы Европы и Ближнего Востока. Это допустимо, так как Европа и Азия не представляют из себя существенно изолированных образований, и их границы не могли сильно затруднить взаимопроникновение при миграциях.
5. Европа
Графики резко отличаются от предыдущих наличием ярких пиков. Отметим, что максимальные значения для Лиссабона и Варшавы достигаются при k=2, иными словами, сгущение точек лежит в дальней и ближней половине, соответственно. Это объясняется проявлением эффекта изолированной точки, повышающего значения T(n) не только для самой точки, но и для некоторых центральных точек региона (см. рис. 4). Тем не менее, оставим Лиссабон в выборке.
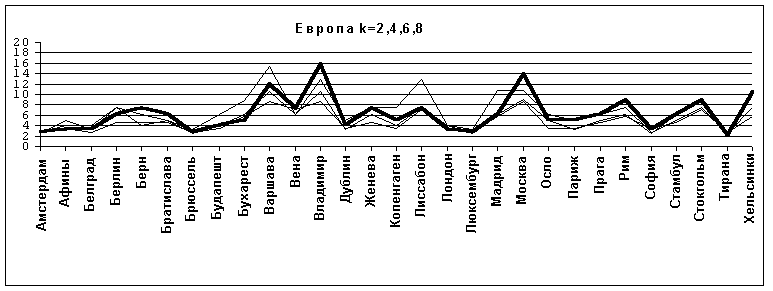
Рис.14
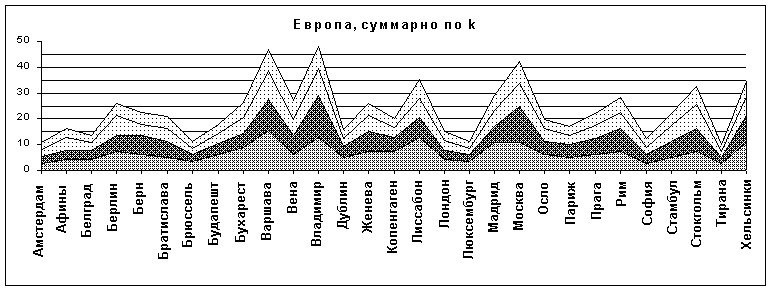
Рис.15
Гораздо интереснее два пика при k=4. Это Владимир и Москва, естественно, (как отмечено в [3, стр .251]) из-за близости расположения в них проявляются одинаковые закономерности. Значение T(n,4) для Владимира превышает 16 (!). Напомним, что функция T(n,k) логорифмическая, и разница в вероятности по сравнению с ближайшим пиком достигает четырех порядков.
6. Европа и Ближний Восток
В этом регионе, в отличие от выборки в [3 стр.251], автор считает возможным исключить точку Кабул, так как поведение функции pop(m) с полным правом позволяет считать ее изолированной, что отражено на графике этой функции на рис.16. Предлагаем сравнить его с графиком изолированной точки рис. 4.
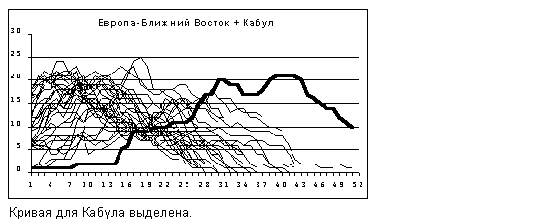
Рис.16
И, наконец,
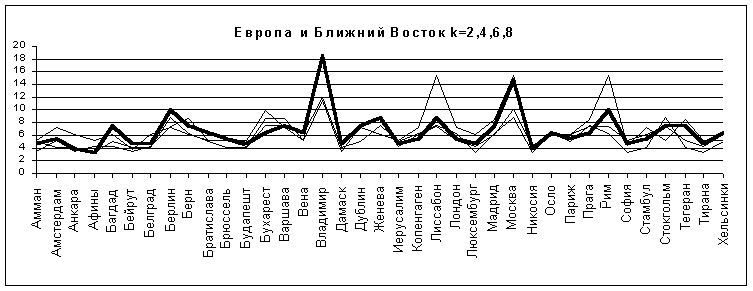
Рис.17
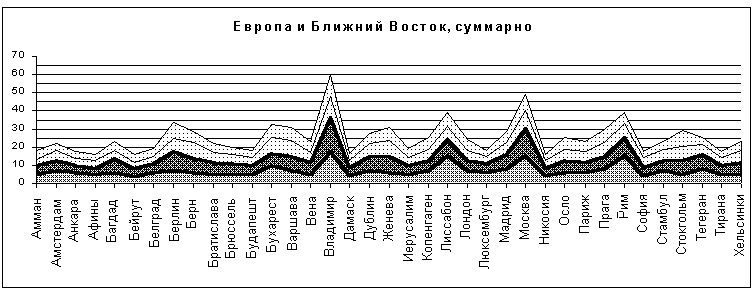
Рис.18
Следовало бы ожидать, что добавление точек Ближнего Востока, как лежащих в стороне от Европы (а среди них могут быть близкие к изолированным), сильно изменит расположение максимумов. В действительности, результат противоположный: максимальное значение для Владимира увеличивается почти до 19, то есть разница с ближайшим пиком составляет уже девять порядков. По поводу максимумов для Лиссабона и Рима справедливо сказанное в п. 5 относительно Лиссабона и Варшавы - Лиссабон так и остался точкой на границе изолированности, а центральная область региона переместилась к юго-востоку (центр тяжести точек первого региона примерно 49°с.ш. 13°в.д., второго - 46°с.ш. 20°в.д.).
Таким образом, необычно большое количество точек этого региона располагается слоем вокруг одной определенной области и вероятность случайного расположения в рамках исходных данных имеет абсолютный минимум.
Автору не удалось найти объективных причин такого расположения точек этого региона.
Заключение части 1
Из изложенного выше автор считает возможным сделать следующие выводы:
1. С точки зрения предложенной методики и выборок, на планете Земля существует особая область, расположенная на Средне-Русской возвышенности в районе современного г. Владимира, характеризующаяся абсолютным максимумом функции T(n,k) , не имеющим объективных обоснований.
2. Для всех регионов, кроме Европы-Ближнего Востока, максимумы имеют объективные географические причины.
3. Автор не согласен с замечанием Г.Н.Носовского и А.Т.Фоменко [3,стр.254] о том, что такое расположение могло возникнуть случайно. Как показано выше, вероятность этой гипотезы минимальна. Распределение столиц этого региона не выглядит ни равномерным, ни случайным.
4. Единственным остающимся разумным объяснением эквидистантного с определенной точностью расположения столиц , по мнению автора, может быть только умысел строителя. В этом случае , полагает автор, чтобы отсчитывать расстояния, прежде надо иметь точку отсчета, иными словами, чтобы провести окружность, сначала надо "поставить циркуль" в уже существующий центр.
Часть 2
Und dort gibt es noch etwas rundes.
J.W.Goehte
Приступая к написанию второй части с примерно годичным перерывом, автор посчитал возможным не менять формулировку выводов первой части, учитывая, что ни методика, ни исходные данные не изменились, и вторую часть можно считать дополнением и уточнением первой.
Постановка задачи, исходные данные
Во второй части автор приступает к тотальному сканированию заинтересовавшего его своей необычностью региона, Европы - Ближнего Востока. При этом используются те же вероятностные функции, что и в первой части. Исходными данными являются координаты Европейско - Ближневосточных столиц, но с одним отличием: к ним добавляются координаты "бегущей точки". На заданном сферическом прямоугольнике (в нашем случае он выбран с координатами от 20 до 80 градусов северной широты, и от 0 до 90 градусов восточной долготы) точка пробегает все значения с шагом 1 градус как по широте, так и по долготе. Все пары координат этой точки образуют сетку 60х90. Далее для каждой из пар подсчитывается значение функции Т, по методике, приведенной в первой части, и полученное значение сопоставляется с координатами узла. Таким образом мы получаем трехмерную поверхность, аргументами которой служит весь набор пар координат "бегущей точки", а функцией - значение Т для каждого аргумента. Отличие методики, от применяемой в части 1, состоит в том, что интервал оценки l (равный Lmax/k в первой части) не вычисляется, а задается явно; в данном случае использовались интервалы 300, 200 и 100 км. Причиной этому служит то, что применение интервала с коэффициентом деления приводит к массовому проявлению "эффекта изолированной точки" и получаемая картина не поддается никакому анализу.
Сканирование региона
На рис.19 приведены результаты исследования региона Европа - Ближний Восток.
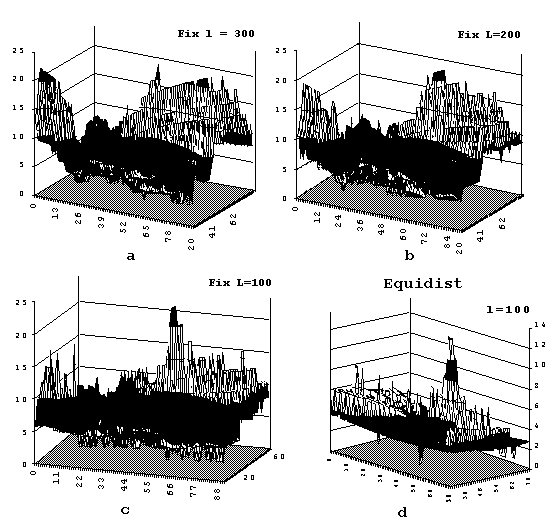
Рис. 19
Рис. 19d показывает, как должна вести себя функция Т при идеально эквидистантном расположении точек (искусственно поставлено 9 точек вокруг центра, который явно выделяется на рисунке.
Рис. 19а, 19b и 19с показывают поведение функции на реальном регионе с параметрами 300, 200 и 100 км соответственно. Как особенно ясно видно из 19с, точки располагаются преимущественно кольцом шириной около 100 км вокруг точки с координатами 53 гр. СШ и 54 гр. ВД, условно обозначаемой далее PUP. Точки располагаются вокруг нее по окружности с радиусом приблизительно 2400 км.
Это позволяет выделить другую, по сравнению с выделенной в первой части область, а именно среднее течение Волги, площадь, примерно ограниченную по линии Самара -- Оренбург -- Уфа -- Казань. Достаточно сравнить рис c и d.
Изменение некоторых параметров и модификация функции Т для исследуемой точки.
Попробуем внести координаты обнаруженной точки в общий список и применим к ней методику части 1. Коэффициент деления возьмем k=4. Результат приведен на рис.20.
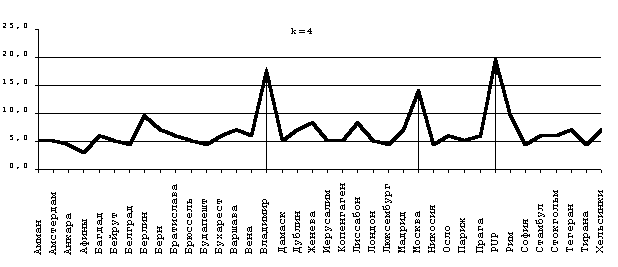
Рис. 20
Как мы видим, минимум вероятности случайного распределения в данной выборке действительно приходится на нее. Установим фиксированный интервал l=200 км. Результат показан на рис.21.
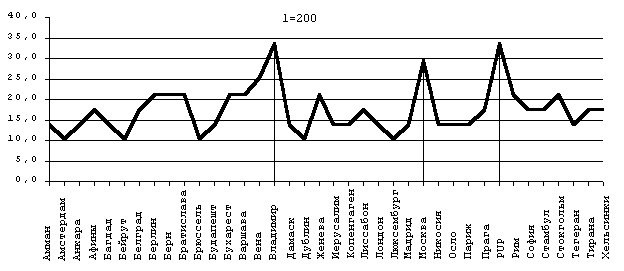
Рис. 21
Наконец модифицируем функцию Т таким образом (-lgP для наглядности остается), чтобы ее значение в данной точке было равно вероятности (при случайном распределении) следующего события: n1 точек попадают в интервал L1 (событие A) и n2 точек попадает в интервал L2 (событие B); интервалы не пересекаются, длины их для простоты берутся одинаковыми (200 км).
Как известно, вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную в предположении, что первое событие уже наступило. Соответствующая формула приведена в Приложении 2.
Результат вычислений по этой формуле приведен на Рис. 22.
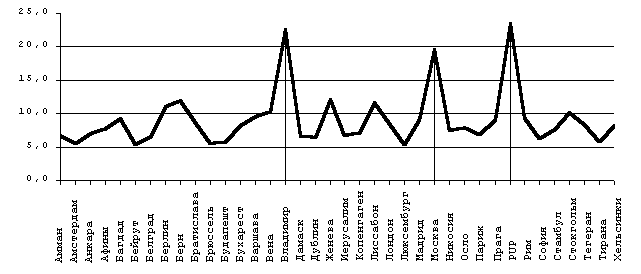
Рис. 22
Фактически, для каждой точки он является ответом на вопрос: какова вероятность того, что при случайном распределении, прочие точки будут сгруппированы вокруг данной в два равных по ширине слоя. И опять-таки на общем фоне неоспоримо выделяются PUP, Владимир и Москва.
Для полноты картины на рис. 23 приводится гистограмма расстояний от точки PUP до прочих городов.

Рис. 23
Заключение части 2
1. Результаты сканирования региона Европа-Ближний Восток полностью подтверждают выводы, сделанные в первой части работы.
2. Теоретический центр должен быть смещен в среднее течение Волги, в район Самары.
3. Реальный центр может отстоять от теоретического на несколько сотен км., т.к. теоретические расстояния берутся по дуге главного круга и, естественно, меньше реальных.
Автор еще раз подчеркивает основной вывод первой части с некоторой коррекцией:
С точки зрения предложенной методики и выборок, на планете Земля существует особая область, расположенная в среднем и верхнем течении р.Волга теоретически с центром в точке с координатами 53 гр. СШ и 54 гр. ВД, характеризующаяся абсолютным максимумом функции T(n,k) , не имеющим объективных обоснований.
Часть 3
- И что же, по вашему мнению, является самым важным
открытием за все эти тринадцать лет?
- Сам факт Посещения.
- Простите?
- Сам факт Посещения является наиболее важным открытием
не только за истекшие тринадцать лет, но и за все время
существования человечества. Не так уж важно, кто были
эти пришельцы. Неважно, откуда они прибыли, зачем
прибыли, почему так недолго пробыли и куда девались потом...
Боюсь, что институту внеземных культур уже никогда больше
не повезет cделать более фундаментальное открытие.
А. и Б. Стругацкие
Автор в любой момент готов выслушать и ответить на пожелания, претензии и критику первых двух частей работы. Третья часть является гипотезой, и поэтому возражения против нее автор считает возможным оставить без внимания. Поскольку официальная история не дает никакого толкования рассмотренному выше факту, а, скорее, даже не подозревает о его существовании, автор позволит себе высказать некоторые небесспорные предположения.
Расположение столиц государств, как наиболее древних городов (в своем большинстве) некоторым образом отражает процесс первоначального массированного заселения региона. Естественно, кто-то там жил и до этого момента, однако крупных населенных пунктов не было. Если расположение большого количества городов подчиняется одной и той же закономерности, можно предположить, что в основном они закладывались почти одновременно (в пределах, возможно, одного столетия, так как вряд ли идея конкретного строительства может продержаться дольше одного - двух поколений строящих). Естественно, из этого ряда могут быть и исключения, то есть некоторые единичные города могли быть построены и раньше.
Расположение городов по окружности вокруг некой компактной области может трактоваться двояко: либо как защитный пояс, либо как фронт распространения (расселения). В данном случае, очевидно, первое предположение не оправдано, как с точки зрения расстояний, так и из-за отсутствия подобной конструкции с противоположных сторон. Наиболее вероятен вариант заселения, причем сознательного, со строительством городов на определенном расстоянии от центральной области. Трудно сказать, представляет ли собой выявленное расположение одну или несколько окружностей. Не исключено, что фронт распространения мог иметь сложную структуру: например, некоторые из рассмотренных точек становились центрами вторичных окружностей. К сожалению, эффекты такого порядка вряд ли удастся обнаружить применяемой методикой.
Распространение идет в широком секторе от северо-запада до юга. Можно предположить, что по каким-то причинам прочие направления не устраивали расселяющихся.(Например, северное - из-за климатических условий, юго-восточное, возможно, было уже заселено - ими же, или другими). В любом случае, мы видим на карте следы явления континентального масштаба, возможно, того самого Великого Переселения Народов, о котором говорит и официальная история, трактуя его, правда, другим образом.
Можно предположить, что фиксированное расстояние обусловлено фиксированным временем его преодоления. Здесь будет уместно процитировать В.В.Бандуркина:
"... вряд ли кто-то располагал столицы, отмеряя расстояния по карте (да и карт настолько точных тогда, пожалуй, не было). Но механизм возникновения столиц провинций на одинаковых расстояниях от центра могу предложить: средний дневной пробег конного гонца 80 – 100 верст (данные музея коневодства Тимирязевской сельскохозяйственной академии). При таком темпе больше 12 дней человек в седле провести не может (просто, извините, седалище до кости сотрет). Доверять сверхважный документ двум и более гонцам я бы лично не рискнул. Вот и получается, что 1 000 верст – максимальное удаление ставки полководца от столицы Империи. По такому же принципу формировалась и вторая окружность столиц..."
Следует учитывать что по направлениям могли быть (и, скорее всего, были) некоторые промежуточные пункты, не ставшие столицами государств (например, некоторые бывшие губернские центры России). Так или иначе, для наиболее удаленных крупных поселений расстояния от центральной области сознательно выбирались приблизительно равными.
Относительно времени расселения можно высказать следующие суждения: либо оно происходило в дописьменную эпоху (или до существенного распространения письма) и о нем не сохранилось никаких сведений, либо сведения до нас дошли, но в сильно искаженном виде и рассматриваются в рамках такой исторической концепции, которая не позволяет их опознать.
Также надо иметь в виду, что официальные даты основания городов (за исключением построенных в хорошо документированное время), как правило, не совпадают со временем первоначального заселения конкретного места (например, по официальной легенде основания Москвы, на ее месте уже было некое поселение). Кроме того, во время междуусобных войн ничто не мешало очередному победителю отстроить захваченный и разрушенный город заново, назвать его произвольным именем и считать этот момент основанием города. Единственное, что при этом сохранялось, это само МЕСТО расположения.
О национальной принадлежности расселявшейся группы вряд ли имеет смысл говорить, не исключено, что такого понятия еще не существовало (это может быть справедливым и для второго варианта). Второй вариант предполагает некоторые следы в письменных источниках. Он хорошо согласуется с гипотезой А.Т.Фоменко об экспансии Руси-Орды в западном направлении. В этом случае не исключено, что искомый след просматривается в сказаниях Ветхого Завета, сведениях о вторжении "варваров" и т.п.
Надо отметить, что само название "Русь-Орда" условно, самоидентификация этого образования пока неизвестна. Можно предположить, что в него входили общности, принадлежащие к индо-европейской, алтайской, хамито-семитской языковым группам (следы этого, возможно, еще просматриваются в "Хожении" А. Никитина, простого тверского купца, занесенного в Индию волей случая и, тем не менее, прекрасно общавшегося там без переводчика, причем не только на торговые темы).
Центральная область расселения хорошо совпадает с локализацией легендарного Светлого Ирия (Рая) на южном Урале, см. работу Staff&Co "Анализируя Асова". На карте Гийома де Лиля 1707-9г в этой области располагаются Roy de Casan и Duche de Bulgar (см. на том же сайте: "Коллекция карт Великой Татарии").
Автор здесь намеренно избегает терминов "колонизация", "Империя" и т.п., так как из рассмотренной картины не просматривается структура общественного образования осуществившего достаточно сложный процесс расселения. Однако отметим, что это образование по уровню технической и военной организации явно превосходило уровень местного населения. Можно даже предположить, что до закладки прообразов столиц, существенного количества крупных поселений в рассматриваемой местности не было, либо они были уничтожены или преобразованы переселенцами.
Вывод
В любом случае, картина развития цивилизации данного региона, обрисованная официальной историей (библейские государства, древняя Греция с Афинами, древний Рим и колонизация полудикой Европы и т.п.) полностью противоречит картине, которую мы можем до настоящего времени можем наблюдать на поверхности Европейско-Ближневосточного региона.
Напротив, в рамках гипотезы А.Т.Фоменко отмеченные факты получают удовлетворительную интерпретацию.
Приложение 1: Таблицы расстояний в данном варианте статьи не приводится из-за большого объема и малой информативности для неспециалистов. Ознакомиться с ними можно на сайте автора http://vzh.by.ru/
Суть работы в определении вероятности случайного распределения точек, относительно выбранной, ПО РАССТОЯНИЮ. Направление (азимут) во внимание не принимается. В силу этого, мы имеем право спроектировать все точки на отрезок, началом которого служит выбранная точка, концом - точка, находящаяся на наибольшем удалении, прочие точки располагаются между ними на соответствующих расстояниях. Расстояния (в км.) определяются по поверхности шара по формуле:
S= R * arccos (sin(e1)*sin(e2)+cos(e1)*cos(e2)+cos(d1-d2)) ,
где R - средний радиус одной из широко испльзующихся моделей Земли (в км), ei и di -широта и долгота соотв. точек (в радианах).
Пусть у нас есть N+2 точек (2 определяют начало и конец отрезка длиной L). Выделим на отрезке интервал l=L/k, где k - коэффициент деления, параметр, который мы можем в процессе рассмотрения менять (в качестве параметра можно использовать и непосредственное значение l). Очевидно, вероятность попадания одной точки на l равна p=l/L. Вероятность попадания m точек определяется формулой Бернулли:
P = CNm * pm * (1-p)N-m ,
где N - количество испытаний (точек), m1 - количество точек, попавших в интервал.
Вероятность совместного появления двух событий (вероятность p для обоих считаем одинаковой) определяется формулой:
P = CNm1 * pm1 * (1-p)N-m1 * CN-m1m2 * pm2 * (1-p)N-m1-m2 ,
где N - количество испытаний, m1 - количество точек, попавших в первый интервал сгущения, m2 - количество точек, попавших во второй интервал сгущения.
Очевидно, чтобы получить какой либо осмысленный результат, выборка должна охватывать точки, принадлежащие к некоторому классу. В качестве наиболее очевидного выбраны СТОЛИЦЫ государств (для США - штатов ). Желающие могут повторить расчеты на других выборках, например, города, начинающиеся на букву М и т.п.
Так как рассчитанные вероятности отличаются на порядки, для наглядности предлагается ввести функцию T=-lnP, вид которой позволяет отобразить результаты на одном листе. Абсолютный максимум Функции Т, означает, что гипотеза о случайном распределении точек вокруг данной ИМЕЕТ МИНИМАЛЬНУЮ ВЕРОЯТНОСТЬ. Иначе говоря, гипотеза о неслучайном распределении ИМЕЕТ МАКСИМАЛЬНУЮ ВЕРОЯТНОСТЬ. Закономерность в данном случае очевидна: преимущественное расположение точек вокруг данной на расстоянии S +- l/2.
Строгое толкование этого факта автор предоставляет читателям.
Литература:
1. Под ред. С.И.Сергеевой "Атлас мира" тт 1-4 ГУГиК М. 1981
2. Под ред. Л.Н.Паффенгольца "Геологический словарь" тт 1,2 Недра М. 1973
3. Г.В.Носовский А.Т.Фоменко "Библейская Русь" т 2 Факториал М. 1998
4. М.Я. Выгодский "Справочник по элементарной математике" ГИФМЛ М. 1963
5. Под ред. К.П.Яковлева "Краткий физико-технический справочник" т 1 ГИФМЛ М.1960
6. В.Е.Гмурман "Теория вероятности и мат. статистика" Высшая школа М.1999
7. Используются ссылки на сайт Staff&Co http://www.chat.ru/~staff1/pagebuilder/ooo.html
© В.П.Жарков 2001
|
|